5 Semantics and Semantic Interpretation
This chapter will consider how to capture the meanings that words and structures express, which is called semantics. The goal of a meaning representation is to provide a mapping between expressions of language to concepts in some computational model of a domain, which might be specified as a software application or as a set of well-formed formulas in a logic (or as some hybrid of the two, such as an AI frame system[1], [2], [3]). A reason to do semantic processing is that people can use a variety of expressions to describe the same situation. Having a semantic representation allows us to generalize away from the specific words and draw insights over the concepts to which they correspond. This makes it easier to store information in databases, which have a fixed structure. It also allows the reader or listener to connect what the language says with what they already know or believe.
As an example, consider what we might learn from the following sentence: “Malaysia’s crude palm oil output is estimated to have risen by up to six percent.”[4]. This sentence tells the reader (among other things) that countries have associated manufacturing and agricultural outputs, that one of Malaysia’s outputs is “crude palm oil”, and that some estimated measure of that output for some time period increased by “six percent or less”. However, the reader might need to clarify what type of measure (e.g., volume or value) and what time period (e.g., month, year, or decade), or they might rely on background knowledge, such as knowing that this was an annual report of production volumes.
Semantic processing can be a precursor to later processes, such as question answering or knowledge acquisition (i.e., mapping unstructured content into structured content), which may involve additional processing to recover additional indirect (implied) aspects of meaning. The primary issues of concern for semantics are deciding a) what information needs to be represented b) what the target semantic representations are, including the valid mappings from input to output and c) what processing method can be used to map the input to the target representation.
Decisions about what needs to be represented will depend on the target task, but there are four main types of information that are typically included. These four things are:
- the entities that are being described,
- the types of events that are being mentioned and the roles that the entities fulfill with respect to the event,
- the type of propositional attitude that a sentence expresses, such as a statement, question, or request, and
- the intended word senses for each occurrence of a word in a sentence.
This information is determined by the noun phrases, the verb phrases, the overall sentence, and the general context. The background for mapping these linguistic structures to what needs to be represented comes from linguistics and the philosophy of language.
The target semantic representation will also depend on the target task. Shallow representations might identify the main verb and the spans of text that correspond to the entities that fulfill the functional parameters or semantic roles associated with the intended meaning of the verb. Deeper representations include the main verb, its semantic roles and the deeper semantics of the entities themselves, which might involve quantification, type restrictions, and various types of modifiers. The representation frameworks used for Natural Language semantics include formal logics, frame languages, and graph-based languages. Shallow representations might be sufficient for tasks related to mapping unstructured content into a structured representation (e.g. knowledge acquisition). Deep representations would be useful for tasks that require being able to go from a structured representation back into text via natural language generation, such as report generation or question answering from a knowledge base.
The processing methods for mapping raw text to a target representation will depend on the overall processing framework and the target representations. A basic approach is to write machine-readable rules that specify all the intended mappings explicitly and then create an algorithm for performing the mappings. An alternative is to express the rules as human-readable guidelines for annotation by people, have people create a corpus of annotated structures using an authoring tool, and then train classifiers to automatically select annotations for similar unlabeled data. The classifier approach can be used for either shallow representations or for subtasks of a deeper semantic analysis (such as identifying the type and boundaries of named entities or semantic roles) that can be combined to build up more complex semantic representations.
We will now consider each of these three aspects in greater detail. It should be noted that for some problems, a deep semantics such as described here is not necessary. In Chapter 8, we will discuss information extraction, which maps free text onto data structures without trying to provide any mapping between expressions in language and entities or events in an underlying model of a task domain or the “real world.”
5.1 Information to be Represented
For sentences that are not specific to any domain, the most common approach to semantics is to focus on the verbs and how they are used to describe events, with some attention to the use of quantifiers (such as “a few”, “many” or “all”) to specify the entities that participate in those events. These models follow from work in linguistics (e.g. case grammars and theta roles) and philosophy (e.g., Montague Semantics[5] and Generalized Quantifiers[6]). Four types of information are identified to represent the meaning of individual sentences.
First, it is useful to know what entities are being described. These correspond to individuals or sets of individuals in the real world, that are specified using (possibly complex) quantifiers. Entities can be identified by their names (such as a sequence of proper nouns), by some complex description (such as a noun phrase that includes a head noun, a determiner, and various types of restrictive modifiers including possessive phrases, adjectives, nouns, prepositional phrases, and relative clauses), or by a pronoun.
Second, it is useful to know what types of events or states are being mentioned and their semantic roles, which is determined by our understanding of verbs and their senses, including their required arguments and typical modifiers. For example, the sentence “The duck ate a bug.” describes an eating event that involved a duck as eater and a bug as the thing that was eaten. The most complete source of this information is the Unified Verb Index.
Third, semantic analysis might also consider what type of propositional attitude a sentence expresses, such as a statement, question, or request. The type of behavior can be determined by whether there are “wh” words in the sentence or some other special syntax (such as a sentence that begins with either an auxiliary or untensed main verb). These three types of information are represented together, as expressions in a logic or some variant.
Fourth, word sense discrimination determines what words senses are intended for tokens of a sentence. Discriminating among the possible senses of a word involves selecting a label from a given set (that is, a classification task). Alternatively, one can use a distributed representation of words, which are created using vectors of numerical values that are learned to accurately predict similarity and differences among words. One might also combine a symbolic label and a vector.
In some specialized domains, the primary focus is on the specification of ontologies of objects rather than events, where objects may have very complex requirements for their attributes. Ontologies specify definitions of concepts, place them into a hierarchy of subtypes, and define the various types of relations that they hold (e.g., “subclass-of”, “instance-of”, “part-of”, etc.), and any restrictions on these relations. For example, in the domain of anatomy, there is a distinction between “shared” and “unshared” body parts. Below is an explanation from a paper describing one such ontology:
“In modeling anatomy, we not only need to represent the part-of relations, but also we need to qualify relations between a part and a whole with additional attributes. For example, parts of an organ can be shared (that is, they belong to several anatomical entities) or unshared (they belong to one anatomical entity). Blood vessels and nerves that branch within a muscle must be considered a part of both that muscle and the vascular or neural trees to which they belong. In contrast, the fleshy part of the muscle (made of muscle tissue) and the tendon (made of connective tissue) are unshared”. [7]
To represent this distinction properly, the researchers chose to “reify” the “has-parts” relation (which means defining it as a metaclass) and then create different instances of the “has-parts” relation for tendons (unshared) versus blood vessels (shared). Figure 5.1 shows a fragment of an ontology for defining a tendon, which is a type of tissue that connects a muscle to a bone. When the sentences describing a domain focus on the objects, the natural approach is to use a language that is specialized for this task, such as Description Logic[8] which is the formal basis for popular ontology tools, such as Protégé[9].
 |
5.1.1 Case Grammar, Events, and Semantic Roles
Theories for what a semantics for natural language sentences should include have their basis in what linguists call a “case grammar”. Case grammars describe the different roles that are associated with different verbs or types of verbs, for example action verbs have an agent and transitive verbs have a direct object, whose role might be described as either the theme or the patient depending on whether the verb affects the object in some way. Case grammars differ from typical representations given in a logic, where one might represent different types of events using different predicate symbols, where each predicate symbol is predefined to have a fixed number of arguments, each of which occurs in a fixed order. For example, the sentence “Rico visited Milwaukee.” might be represented in a logic as “visit(Rico, Milwaukee)”. The arguments of these predicates are terms in the logic, which can be either variables bound by quantifiers, or constants which name particular individuals in the domain. However, verbs can have both required arguments and optional modifiers. Case grammars involve naming the sets of required and modifying roles for each sense of a verb explicitly, for example “[Agent Rico]” or “[Location Milwaukee]”. This is analogous to using keyword arguments in a programming language. Examples of semantic (thematic) roles include “Agent”, which is a sentient being that performs an action and “Patient” which is an affected object of some action. Figures 5.2 to 5.5 include examples of roles, from VerbNet3.3, part of the Unified Verb Index.
| Subject relations | Example |
| Agent ( +intentional, +sentient) | [The cat] chased a mouse. |
| Cause (-intentional, +nonsentient) | [The wind] rattled the windows. |
| Experiencer (+sentient) of perception | [The children] tasted the soup. |
| Pivot | [The bottle] contains seltzer water. |
| Theme (-affected) | [The ball] rolled down the hill. |
| Object relations | Example |
| Attribute | Oil increased in [price]. |
| Beneficiary | Claire sang a song for [her teacher]. |
| Instrument | The chef baked a cake in [the oven]. |
| Material | An oak tree will grow [from an acorn]. |
| Patient (+affected) | The wind destroyed [the sand castles]. |
| Product (+concrete) | Boeing builds [aircraft]. |
| Recipient (+animate) | The teacher gave a book [to a student]. |
| Result | The delay threw the project [into chaos]. |
| Stimulus | The children saw [some clouds]. |
| Theme (-affected) | The boy rolled [the ball] down the hill. |
| Topic | The teacher taught a class [about verbs.] |
|
Place relations |
Example |
| Asset | Carmen purchased a dress [for $50]. |
| Destination | I brought a book [to the meeting]. |
| Extent (+measurable_change) | The top rotates [90 degrees]. |
| Goal | I dedicated myself [to the cause]. |
| Location (+concrete) | I searched [the cave] for treasure. |
| Source | The cleaner removes stains [from clothing]. |
| Value (+scale) | He put the price [at 10 dollars]. |
| Temporal relations | Example |
| Time | He was happy [after receiving his marks]. |
| Duration | The class continued [for two hours]. |
The set of roles associated with a verb by a case grammar are called “semantic frames”. In linguistics, there have been several approaches to defining case grammars. The first case grammars were defined by Dr. Charles J. Fillmore in 1968, in his “The Case for Case”. This work defined commonly occurring cases such as Agent, Object, Benefactor, Location, and Instrument, and provided examples for a small set of verbs for illustration. In 1997, Fillmore began the FrameNet project, a more comprehensive, data-driven effort to define a hierarchy of semantic frames and create a corpus of sentences annotated with semantic roles. FrameNet now includes over 1200 different frames. Software for labelling sentences with FrameNet roles is included in the Natural Language Toolkit. FrameNet is now also part of a larger resource called the Unified Verb Index (UVI). The UVI also includes verb types and annotated text from PropBank, OntoNotes, and VerbNet. The UVI is maintained by the creators of VerbNet at the University of Colorado.
There is an ISO standard for semantic roles which is part of ISO standard 24617, which is a standard for Language resource management — Semantic annotation framework (SemAF). When complete, ISO 24617 will consist of eight parts, of which the following six were the first to be completed:
— Part 1: Time and events (SemAF-Time, ISO-TimeML)
— Part 2: Dialogue acts
— Part 4: Semantic roles (SemAF-SR)
— Part 5: Discourse structure (SemAF-DS)
— Part 7: Spatial information (ISO-Space)
The last parts to be finalized are Part 8: Semantic relations in discourse (SemAF-DRel) and Part 6: Principles of semantic annotation (SemAF-Basics).
5.1.2 Quantification and Scoping
Quantifiers allow one to describe the properties of individuals and sets. In a first order logic of mathematics, there are just two quantifiers, the existential and the universal, and they bind only terms, which are expressions that denote individuals in the domain. Quantifiers introduce an additional type of ambiguity, related to the set of relations over which they bind variables, known as the “scope” of the quantifier. For example, the sentence “Every cat chased a mouse” might mean either that several cats all chased the same mouse, or each cat chased their own personal favorite mouse. Natural language systems can choose to leave quantifiers unscoped or to make a guess based on domain-specific knowledge. Other mechanisms are needed to address scoping across multiple sentences (e.g., some graphical representations use structure sharing, where each entity corresponds to a unique structure and all references to it point back to this same structure.)
The types of quantification that people express in natural language can be much more diverse than mere existence or universality, however. Natural language quantifiers can specify the size of a set at various levels of precision (e.g., “Exactly one”, “At least two”, or “Most”) and they can specify a wide variety of type constraints, such as “most bears”, “most hungry bears”, “most bears that originated from Asia”. To address this variety, the representation of semantics for natural language often involves a mechanism known as “Generalized Quantifiers”[10]. A generalized quantifier consists of the quantifier name, a set of quantified variables, and a constraint, which is a well-formed expression that uses the given variables. These quantifiers and property constraints will hold over any expressions within their scope. For example, “Most small dogs like toys” could be expressed in a logical framework as [Most x, small(x) and dog(x) [All y toys(y): like(x,y)]]. The interpretation of such quantifiers must be defined as some function, which might depend on the domain. For example, one might define “most” as either “more than 50%” or as “more than 60%”. In some ontology tools, these are defined as “role-bounded” quantifiers (e.g., in Protege.)
5.2 Computational Frameworks for Semantics
There are two broad types of semantic frameworks: domain dependent and domain independent. Domain dependent semantics might be considered a mix of semantics and pragmatics – sentences are used to do something so the meaning is the procedure call or query that one would execute to do it. For this reason, these representations are sometimes also called Procedural Semantics[11],[12]. Domain-independent semantics includes identifying the actions, participants, and objects described in language, and possibly other important information, such as when an event occurred and the manner or location in which it occurred. It may also include the interpretation of quantifiers to allow one to select the appropriate set of participants and objects. These representations might be used for a variety of applications, such as machine translation, knowledge acquisition (i.e., learning by reading), question answering, or the control of software. Domain independent semantics typically use some variant of mathematical logic or a graph-based equivalent.
5.2.1 Procedural Semantics
The notion of a procedural semantics was first conceived to describe the compilation and execution of computer programs when programming was still new. In the 1970’s, psychologists, including George A. Miller[13] and Philip Johnson-Laird[14], described how this metaphor might better describe how language is used to communicate as it offered a uniform framework for describing how it is used “to make statements, to ask questions and to answer them, to make requests, and even to express invocations and imprecations” – unlike formal logics which ultimately reduce the meaning of all sentences to one of either “true” or “false”. Of course, there is a total lack of uniformity across implementations, as it depends on how the software application has been defined. Figure 5.6 shows two possible procedural semantics for the query, “Find all customers with last name of Smith.”, one as a database query in the Structured Query Language (SQL), and one implemented as a user-defined function in Python.
|
Sentence: Find all customers with last name of Smith |
|
SQL: SELECT * FROM Customers WHERE Last_Name=’Smith’ |
|
Python: Customers.retrieveRows(last_name=”Smith”) |
For SQL, we must assume that a database has been defined such that we can select columns from a table (called Customers) for rows where the Last_Name column (or relation) has ‘Smith’ for its value. For the Python expression we need to have an object with a defined member function that allows the keyword argument “last_name”. Until recently, creating procedural semantics had only limited appeal to developers because the difficulty of using natural language to express commands did not justify the costs. However, the rise in chatbots and other applications that might be accessed by voice (such as smart speakers) creates new opportunities for considering procedural semantics, or procedural semantics intermediated by a domain independent semantics.
5.2.2 Methods for Creating Procedural Semantics
Procedural semantics can be created either using rule-based methods or by annotating a corpus with the target representation and then training a classifier. When the range of expressions is small, either approach is reasonable. For example, one can associate semantic annotations with particular parse trees by creating context free grammar rules with semantic features. Then, these annotations can be used either during a parse, as each structure is completed, or afterwards by traversing complete parse trees.
As an example, we will consider mapping queries to SQL where “city_table” is a table of cities, countries and populations (shown in Figure 5.7)
| City | Country | Population |
| Calgary | Canada | 1238 |
| Montreal | Canada | 3519 |
| Toronto | Canada | 5429 |
| Vancouver | Canada | 2264 |
| Mexico City | Mexico | 8851 |
| Ecatepec | Mexico | 1655 |
| Guadalajara | Mexico | 1495 |
| Puebla | Mexico | 1434 |
| New York | United_States | 8623 |
| Los Angeles | United_States | 4000 |
| Chicago | United_States | 2716 |
| Houston | United_States | 2312 |
Figure 5.8 gives a set of CFG grammar rules with semantic features for creating SQL statements for queries like “What cities are located in Canada?” or “In what country is Houston?” where the target representations would be “SELECT City FROM city_table WHERE Country = ‘Canada’ ” and “SELECT Country FROM city_table WHERE City = ‘Houston’ ”, respectively.
|
|
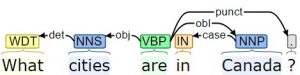
These rules are for a constituency–based grammar, however, a similar approach could be used for creating a semantic representation by traversing a dependency parse. Figure 5.9 shows dependency structures for two similar queries about the cities in Canada.
|
|
|
|
Notice that they both contain the dependencies “det” and “case”. Thus, the result for “cities” and “in Canada” would be SEM (det (WDT, cities)) = “SELECT Cities from city_table WHERE” and SEM(case(IN, Canada)) = “Country = Canada”, respectively.
There are several existing corpora that include paired natural language sentences and SQL queries. One of the largest is the WikiSQL dataset which contains 80,654 pairs of the NL sentence-SQL query derived from 24,241 Wikipedia tables. There is also the Stack Exchange Natural Language Interface to Database (SENLIDB) corpus, which includes 24,890 NL sentence-SQL query pairs constructed using the Stack Exchange API. At the same time, new formats for databases are emerging, including “Graph Databases”, which are optimized for retrieving relationship triples along with associated properties[15],[16]. They also support a query language, Cypher, that is much closer to natural language than SQL, making it more straightforward to map NL sentences onto graph database languages[17]. Figure 5.10 shows an example of a query and an assertion in Cypher.
|
MATCH (:Person {name: ‘Jennifer’})–[:WORKS_FOR]->(company:Company) RETURN company.name Cypher query for “What is the name of the company that Jennifer works for?” |
|
MATCH (jennifer:Person {name: ‘Jennifer’}) MATCH (mark:Person {name: ‘Mark’}) CREATE (jennifer)–[rel:IS_FRIENDS_WITH]->(mark) Cypher assertion that “Jennifer is friends with Mark” |
Procedural semantics are possible for very restricted domains, but quickly become cumbersome and hard to maintain. People will naturally express the same idea in many different ways and so it is useful to consider approaches that generalize more easily, which is one of the goals of a domain independent representation.
5.3 Domain Independent Frameworks
Domain independent semantics tries to capture the type of state or event and its structure, which includes identifying the semantic roles associated with the event where the core roles would be action, subject, and object. It sometimes also tries to address the interpretation of quantifiers. Domain independent semantics are normally also compositional, which means they can be built up incrementally, with general mappings between corresponding syntactic and semantic constituent types. Composition can be defined formally, using the formalism of the lambda calculus[18], or procedurally, by providing explicit rules for composing objects of various types. The result can be either a well-formed expression in a logic, as an expression in an artificial intelligence frame language resembling a logic (sometimes also called a “quasi-logical form”) or as a graph. Graph-based representations, also known as “semantic networks”, offer many advantages, as they tend to be both more expressive than logic and more efficient, because their structure facilitates inference and supports sharing of structures across phrases and sentences.
5.3.1 Using First Order Predicate Logic for NL Semantics
Formal logics have a well-defined syntax, which includes the legal symbols for terms, relations, quantifiers, operators, conjunctions, and functions and how they can be combined. Well-formed expressions are defined recursively. Terms can be constants, variables, or the application of an n-ary function symbol to exactly n terms. Atomic formulas consist of an n-ary relation symbol with exactly n terms as arguments. (If a logic includes the equality symbol then termi = termj is also a legal atomic formula.) Legal non-atomic formulas can be created by any of the following, where ¬ is the negation symbol (i.e., “not”), ˅ is the symbol for disjunction (“or”), ˄ is the symbol for conjunction (“and”), Ǝ is the existential quantifier (“there exists”), and ∀ is the universal quantifier (“for all”).
- If α is a formula then so is ¬α
- If α and β are formulas then so is α ˅ β and α ˄ β
- If x is a variable and α is a formula then so is Ǝx.α and ∀x.α
Logic does not have a way of expressing the difference between statements and questions so logical frameworks for natural language sometimes add extra logical operators to describe the pragmatic force indicated by the syntax – such as ask, tell, or request. Logical notions of conjunction and quantification are also not always a good fit for natural language.
5.3.2 Compositionality in Logic-Based Representations
Domain independent semantics generally strive to be compositional, which in practice means that there is a consistent mapping between words and syntactic constituents and well-formed expressions in the semantic language. Most logical frameworks that support compositionality derive their mappings from Richard Montague[19] who first described the idea of using the lambda calculus as a mechanism for representing quantifiers and words that have complements. Subsequent work by others[20], [21] also clarified and promoted this approach among linguists.
Lambda expressions are function abstractions that can be applied to their arguments and then reduced, to perform substitutions for the lambda-bound variables. For example, λx: (λy: loves (x,y) (Milwaukee)) = λx: loves (x, Milwaukee). Each lambda symbol can bind one or more variables, corresponding to a function that takes one of more arguments. With multiple lambda-bound variables, expressions may be nested, and then evaluated from the inside out, or a single lambda can bind multiple variables, in which case the order of values will determine to which variable they are bound, proceeding from left to right. Syntax for creating lambda expressions exists in Python, as “lambda”, and in NLTK, using a slash operator, “\”. Figure 5.11 shows what happens when lambdas with multiple variables versus multiple nested single variable lambdas are reduced using the NLTK lambda-reduction function, “simplify()”: in each example, x1 is the unreduced lamda expression and x2 is the equivalent reduced, and we show their equality explicitly.
 |
There are two special cases. If the sentence within the scope of a lambda variable includes the same variable as one in its argument, then the variables in the argument should be renamed to eliminate the clash. The other special case is when the expression within the scope of a lambda involves what is known as “intensionality”. Sentences that talk about things that might not be true in the world right now, such as statements about the past, statements that include a modal operator (e.g., “it is possible”), statements that include counterfactuals, and statements of “belief”, such as “Rex believes that the cat is hungry.” all require special care to separate what is true in the world versus some context of an alternate time, of the mental state of some agent, etc. Since the logics for these are quite complex and the circumstances for needing them rare, here we will consider only sentences that do not involve intensionality. In fact, the complexity of representing intensional contexts in logic is one of the reasons that researchers cite for using graph-based representations (which we consider later), as graphs can be partitioned to define different contexts explicitly. Figure 5.12 shows some example mappings used for compositional semantics and the lambda reductions used to reach the final form.
5.3.2.1 Linguistic and Logical Magic
Note that to combine multiple predicates at the same level via conjunction one must introduce a function to combine their semantics. Here we will call that function UNIFY_AND_CONJOIN. The intended result is to replace the variables in the predicates with the same (unique) lambda variable and to connect them using a conjunction symbol (and). The lambda variable will be used to substitute a variable from some other part of the sentence when combined with the conjunction.
|
Function with example parameters |
Result |
|
UNIFY_AND_CONJOIN((x, P1(x)), (y, P2(y))) |
(λx1, [P1(x1) and P2(x1)]) |
|
RAISE_QUANT([S X NP Y]) |
[S NP [S X ei Y]] |
|
RAISE_INFL([S NP INFL X]) |
[ S INFL [S NP X ]] |
|
ONLY_ONE(y,P(y)) |
Ǝy P(y) and ∀z P(z) ⟶ x = y |
Other necessary bits of magic include functions for raising quantifiers and negation (NEG) and tense (called “INFL”) to the front of an expression. Raising INFL also assumes that either there were explicit words, such as “not” or “did”, or that the parser creates “fake” words for ones given as a prefix (e.g., un-) or suffix (e.g., -ed) that it puts ahead of the verb. We can take the same approach when FOL is tricky, such as using equality to say that “there exists only one” of something. Figure 5.12 shows the arguments and results for several special functions that we might use to make a semantics for sentences based on logic more compositional.
In a logic, we must also assume that we represent verbs using a precise number of arguments in a precise order. As an alternative, one could represent the semantics of verbs by adding a term to represent the event and conjoining separate predicates for each of the semantic roles as in: λx: λy: λz: ∃ ev1: [gives (ev1, x,y, z) and agent(ev1,x) and recipient(ev1,y) and theme(ev1,z)]. Figure 5.13 shows the mapping between many common types of expressions in natural language, and a representation in a first order logic that includes lambda expressions.
|
Natural language types |
Logical type |
|
Proper noun |
A term expressed as either a constant, e.g., Ashley or a functional expression, e.g., named_entity(‘Ashley’) |
|
Adjectives and common nouns that occur with determiners |
Lambda expressions with one variable: λx: cat (x), λx: grey(x), |
|
Determiner |
Lambda expressions with quantifiers, e.g., “a” = λx: Ǝy x(y) where the later substitution with a noun provides the predicate symbol. See below. |
|
Noun phrase of: DT JJ NN Where if DT = a then Q y is Ǝy if DT = all then Qy is ∀y if DT = the then Qy P(y) is ONLY_ONE(y, P(y))) |
A quantified expression, e.g. for “a grey cat” which would be ∃ y [grey(y) and cat (y)] obtained as follows:
λx: Q y x(y) (UNIFY_AND_CONJOIN(SEM(JJ),SEM(NN))) λx: ∃y: x(y) (UNIFY_AND_CONJOIN((x, grey(x)), (y, cat (y)))) λx: ∃y x(y) (λx1, [grey(x1) and cat (x1)]) ∃ y (λx1, [grey(x1) and cat (x1)]) (y) ∃ y [grey(y) and cat (y)] |
|
Noun phrase with relative clause e.g. DT NN that S |
A quantified expression, e.g., for “a cat that ate a big mouse” which would be λx: Q y x(y) (UNIFY_AND_CONJOIN(SEM(NN),SEM(S)) obtained as follows: λx: Ǝy x(y) (UNIFY_AND_CONJOIN((x1, cat(x1)), (x2, Ǝz [big(z) and mouse (z) and ate(x2,z)]))) λx: Ǝy x(y) (λu cat(u) and Ǝz [big(z) and mouse (z) and ate(u,z)]) Ǝy (λu cat(u) and Ǝz [big(z) and mouse (z) and ate(u,z)) (y) Ǝy (cat(y) and Ǝz [big(z) and mouse (z) and ate(y,z)]) |
|
Verbs of N arguments (including the subject) |
N nested Lambda expressions, expressed with N separate variables, e.g., for “sleep” or “eats” λx: sleep(x); λy: λx: eats (x,y); λz: λy: λx: gives (x, y, z) |
|
Verb phrase (transitive) RAISE_QUANT( V NP) = NP [ V ei] |
A lambda expression with a raised quantified expression, λx NP [ verb (x,y) (ei)] where ei is the result of quantifier raising, e.g. for “chases a mouse” which would be λx: (λw: Ǝy mouse(y) andchases (x,w)) (y) λx: Ǝy mouse(y) and chases (x,y) |
|
Verb phrase (ditransitive) RAISE_QUANT( V NP1 ) NP2 = NP1, RAISE_QUANT(V NP2) = NP1 NP2 (V e1 e2) |
A lambda expression for a quantified expression,NP1 and [NP2 [λx verb (x, e1, e2)]] e.g., “gave a girl a book.” λx Ǝy [girl(y) and [Ǝz book (z) and gave(x, y, z)]] |
|
Conjoined VP : VP CC VP |
[[VP]] and [[VP]] where [[ X]] gives the semantics of X |
|
Sentence (NP VP) |
λx: x (NP), e.g. “Ashley sleeps.”, NP = Ashley and VP = λz sleep(z) λx: sleep(x) (Ashley) which reduces to sleeps(Ashley) |
|
Sentence NP NPr1 VP where NPr1 is a previously raised NP |
λx Qy Ry and P(x, y)(NP), e.g. “Susan owns a grey cat.” λx Ǝy [grey(y) and cat (y) and owns(x, y)](Susan) Ǝy [grey(y) and cat (y) and owns(Susan, y)
|
|
Sentence NP NPr1 NPr2VP where NPri are previously raised NP |
Q1yRy and Q2z Rz and λx P(x, y, z)(NP) e.g. “Sy gave a girl a book.” λx Ǝy[girl(y) and Ǝz book (z) and gave(x, y, z)](Sy) Ǝy [girl(y) and Ǝz book (z) and gave(Sy, y,z)] |
|
Conjoined sentence: S CC S |
[[S]] and [[S]] where [[ X]] gives the semantics of X |
5.3.2.2 Referring Expressions
Pure FOL, even with lambda expressions, does not fully capture the meaning of referring expressions such as pronouns, proper names, and definite descriptions (such as “the cat”), when we consider what would be needed by a database or a knowledge base (KB). A backend representation structure must be able to link referential expressions, such as “the cat” or “a cat”, to some entity in the KB, either existing (“the”) or newly asserted “a”. Also, it is not always sufficient to use a constant for named entities, e.g., [[Susan]] = susan. Using a constant like this assumes uniqueness (e.g., that there is only one person named Susan), when in reality there are millions of people who share that name. At an abstract level, what we need is a representation of entities, distinct from the expressions (strings) used to name them and we need functions to map between the expressions at the logical level, with those in the underlying KB. We can express this at the logical level by defining function symbols that invoke these functions at the implementation level, such as Named_entity( “Susan”) or Pronoun( “it”). Then to implement these at the backend we would need to define them with some new ad hoc function or database assertion or query. In Python we might build a dictionary with dynamically created identifiers as keys and asserted relations as values, e.g., relations[cat1] = [grey(cat1), cat(cat1), eat(cat1, mouse1)], when “a grey cat ate a mouse” is mentioned. Or we might use a database language, such as Cypher, with expressions like CREATE (susan:Person {name: ‘Susan’}) or MATCH (:Person {name: ‘Susan’}), respectively, when Susan is mentioned. Including KB entities within the semantics would also require making a change to representations involving an existential quantifier, where we remove the quantifier and substitute for the variable a new constant corresponding to the unnamed individual for which the predicate is true. In logic this notion is accomplished via a “skolem function”; for an NL semantics one might use an ad hoc function to create new symbols on the fly[22]. And, with possibly multiple symbols corresponding to the same real-world entity, a logic or KB would also need an equality operator, e.g., susan1 = susan2 or owl.sameAs(susan1,susan2). Similar issues (and solutions) would arise for references to entities that get their meaning from the context, such as indexicals (“I”, “you”, “here”, or “there”) or references that depend on time and location (“the president”, “the teacher”). We will discuss these issues further in Chapter 7, when we consider how multiple sentences taken together form a coherent unit, known as a discourse.
5.3.3 Frame Languages and Logical Equivalents
Although first order logic offers many benefits (such as well-defined semantics and sound and complete inference strategies) they have critical deficiencies when it comes to representing objects, in addition to just referring to individuals as discussed in Section 5.3.2. It is also problematic that, in FOL, all categories and properties of objects are represented by atomic predicates. Description logic (DL)[23] provides a way of relating different predicates as part of their definition, independent of what facts one might assert with them. A DL knowledge base (KB) will include expressions that specify definitions by saying that some atomic concept is equivalent to a complex one. It will also include expressions that give names to partial definitions by saying that an atomic concept is subsumed by another one. Thirdly it will assert properties of individuals. The only types of inference are thus assertion and classification, but knowing whether one has defined a consistent ontology is important for many disciplines. DL systems have been used to create and manage very large ontologies (even millions of concepts). For example, they have been widely used in biology and medicine and many public ontologies exist (e.g., the US NCBO Bioportal lists over 900 public ontologies). DL systems can also provide an object-oriented frontend to a relational database.
The syntax of DL includes three main types: concepts, roles, and constants. In terms of the logic, concept names are unary predicates; however we can specify complex concepts as a conjunctions of simpler ones. Role names are binary predicates, e.g. hasMother(robert,susan). Constants are the names of individuals. One can also specify restrictions on the values of roles, and reify relations to define metaclasses and a metaclass hierarchy. In relation to natural language constituents, common (or category) nouns, such as “dog” are concepts; relational nouns, such as “age”, “parent”, or “area_of_study”, are roles, and proper nouns are constants.
There are four types of logical symbols: punctuation (e.g., round and square brackets), positive integers, concept-forming operators (e.g., ALL, EXISTS, FILLS, AND), and three types of connectives (one concept is subsumed by another (d ⊆ e) ; one concept satisfies the description of another (d ⟶ e); and one concept is equivalent to another (d ≡ e). Atomic concepts, roles, and constants are the only “nonlogical symbols” – that is, ones that the user defines. With these types and symbols, we can now define the well-formed formulas of DL, as shown in Figure 5.14. The rules define valid concepts and three types of sentences. One can say that two concepts are equivalent, using ≡, or that one concept is subsumed by another, using ⊆, or that a given constant (an instance) satisfies the description expressed by a concept, using ⟶.
|
Syntax |
Example |
|---|---|
| Every atomic concept is a concept. | cat |
| If r is a role and d is a concept, then [ALL r d] is a concept. | [ALL :weight cat] |
| If r is a role and n is an integer, then [EXISTS n r] is a concept. | [EXISTS 4 :legs] |
| If r is a role and c is a constant, then [FILLS r c] is a concept. | [FILLS :legs leg1] |
| If d1, …, dk are concepts, then so is [AND d1, …, dk]. | [AND mammal predator [EXISTS 4 :legs] [EXISTS 1 :tail]] |
| If d and e are concepts, then (d ≡ e) is a sentence. | four_legged ≡ [EXISTS 4 :legs] |
| If d and e are concepts, then (d ⊆ e) is a sentence. | cat ⊆ four_legged |
| If c is a constant and d is a concept, then (c ⟶ d) is a sentence. | TardarSauce ⟶ cat |
By default, every DL ontology contains the concept “Thing” as the globally superordinate concept, meaning that all concepts in the ontology are subclasses of “Thing”. The quantifiers each specify particular subsets of the domain. [ALL x y] where x is a role and y is a concept, refers to the subset of all individuals x such that if the pair <x, y> is in the role relation, then y is in the subset corresponding to the description. [EXISTS n x] where n is an integer is a role refers to the subset of individuals x where at least n pairs <x,y> are in the role relation. [FILLS x y] where x is a role and y is a constant, refers to the subset of individuals x, where the pair x and the interpretation of the concept is in the role relation. [AND x1 x2 ..xn] where x1 to xn are concepts, refers to the conjunction of subsets corresponding to each of the component concepts. Figure 5.15 includes examples of DL expressions for some complex concept definitions.
|
“a company with at least 7 directors, whose managers are all women with PhDs, and whose minimum salary is $100/hr” [AND Company [EXISTS 7 :Director] [ALL :Manager [AND Woman [FILLS :Degree PhD] [FILLS :MinSalary ‘$100/hour’]]] |
|
“A dog is among other things a mammal that is a pet and a carnivorous animal whose voice call includes barking” (Dog [AND Mammal Pet CarnivorousAnimal [FILLS :VoiceCall barking]]) |
|
“A FatherOfDaughters is a male with at least one child and all of whose children are female” (FatherOfDaughters ≡ [AND Male [EXISTS 1 :Child] [ALL :Child Female]] ) |
|
“Joe is a FatherOfDaughters and a Surgeon” (joe → [AND FatherOfDaughters Surgeon]]) |
Description logics separate the knowledge one wants to represent from the implementation of underlying inference. Inference services include asserting or classifying objects and performing queries. There is no notion of implication and there are no explicit variables, allowing inference to be highly optimized and efficient. Instead, inferences are implemented using structure matching and subsumption among complex concepts. One concept will subsume all other concepts that include the same, or more specific versions of, its constraints. These processes are made more efficient by first normalizing all the concept definitions so that constraints appear in a canonical order and any information about a particular role is merged together. These aspects are handled by the ontology software systems themselves, rather than coded by the user.
Ontology editing tools are freely available; the most widely used is Protégé, which claims to have over 300,000 registered users. Protégé also allows one to export ontologies into a variety of formats including RDF (Resource Description Framework)[24][25] and its textual format Turtle, OWL (Web Ontology Language)[26], [27], and XML Schema[28], so that the knowledge can be integrated with rule systems or other problem solvers.
Another logical language that captures many aspects of frames is CycL, the language used in the Cyc ontology and knowledge base. The Cyc KB is a resource of real world knowledge in machine-readable format. While early versions of CycL were described as being a frame language, more recent versions are described as a logic that supports frame-like structures and inferences. Cycorp, started by Douglas Lenat in 1984, has been an ongoing project for more than 35 years and they claim that it is now the longest-lived artificial intelligence project[29].
5.3.4 Compositionality using Frame Languages
Compositionality in a frame language can be achieved by mapping the constituent types of syntax to the concepts, roles, and instances of a frame language. For the purposes of illustration, we will consider the mappings from phrase types to frame expressions provided by Graeme Hirst[30] who was the first to specify a correspondence between natural language constituents and the syntax of a frame language, FRAIL[31]. Figure 5.16 shows the mappings for the most common types of phrases. These mappings, like the ones described for mapping phrase constituents to a logic using lambda expressions, were inspired by Montague Semantics. The frame language syntax used here includes symbols for variables and constants, which might name entities, the values of attributes, or instances (e.g., “Newton”, “black”, or cat01); symbols for frame types, which include both entities and actions (e.g., “cat” or “eat”); symbols for slots, which might be properties or semantic roles (e.g., “color” or “agent”); and symbols for frame determiners, which are functions for either storing or querying the frame system. Well-formed frame expressions include frame instances and frame statements (FS), where a FS consists of a frame determiner, a variable, and a frame descriptor that uses that variable. A frame descriptor is a frame symbol and variable along with zero or more slot-filler pairs. A slot-filler pair includes a slot symbol (like a role in Description Logic) and a slot filler which can either be the name of an attribute or a frame statement. The language supported only the storing and retrieving of simple frame descriptions without either a universal quantifier or generalized quantifiers. More complex mappings between natural language expressions and frame constructs have been provided using more expressive graph-based approaches to frames, where the actually mapping is produced by annotating grammar rules with frame assertion and inference operations.
|
Syntactic type and examples |
Frame expression |
Examples |
|---|---|---|
|
Determiner, “the”, “a” |
Frame determiner |
(the ?x), (a ?x) |
|
Common noun, “cat”, ”mat” |
Frame |
(cat ?x), (mat ?x) |
|
Pronoun, “he” |
Frame statement, Instance |
(the ?x (being ?x (gender = male)), man87 |
|
WH Pronoun, “what”, “which” |
Variable |
?wh |
|
Noun phrase, “the cat” |
Frame statement, Instance |
(the ?x (cat ?x)), cat01 |
|
Proper noun phrase, “Newton” |
Frame statement, Instance |
(the ?x (thing ?x (name = Newton)), thing01 |
|
Main verb, “chase”, “sleep” |
Frame |
(chase ?x) , (sleep ?x) |
|
Adjective, “black” |
Slot-filler pair |
(color = black) |
|
Preposition, “on” |
Slot name |
location |
|
Prepositional phrase, “on the mat” |
Slot-filler pair |
(location = mat93) |
|
Auxiliary verb, “was” |
Slot-filler pair |
(tense = past) |
|
Adverb, “quietly” |
Slot-filler pair |
(manner = quietly) |
|
Verb phrase, “chase a mouse” |
Frame descriptor |
(chase ?x (patient = (a ?y (mouse ?y)))) |
|
Clause-end punctuation, “.”, “?” |
Frame determiner |
(a ?x), (question ?x) |
|
Sentence “The cat ate the mouse”, “What did he eat?” |
Frame statement, Instance |
(a ?x (eat ?x (agent = cat01) (patient = mouse19))), (question ?x (eat ?x (agent = cat01) (patient = ?wh ))) |
5.3.5 Graph-Based Representation Frameworks
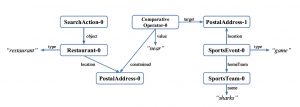
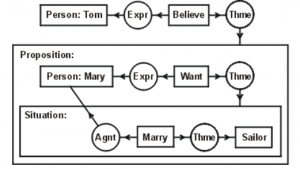
Graph-based representation frameworks for semantics have drawn wider attention with the commercial success of Amazon Alexa[32]. Although application developers define intents in terms of natural language sentences, it was reported in June 2018 that Alexa’s internal representation – before accessing the applications – would use a new graph-based framework called the “Alexa Meaning Representation Language”[33], [34]. Figure 5.17 shows the graph for a request to find a restaurant that includes a complex spatial relation “near the Sharks game”. Graph-based representations of knowledge have had a longstanding following, including The International Conference on Conceptual Structures, which has origins going back to 1986. The focus of the meeting is a semantic framework called Conceptual Graphs. Figure 5.18 shows an example by John Sowa, illustrating one of the three possible interpretations of “Tom believes Mary wants to marry a sailor.” along with its text-based representation in the Conceptual Graph Interchange Format, part of the ISO standard for Common Logic. Other currently active graph-based projects for NL include the FRED machine reading project which generates representations as RDF/OWL ontologies and linked data, and the Cogitant project which distributed libraries for editing Conceptual Graphs. There are also freely available datasets of text annotated with CG that have been used for supervised (reinforcement) learning[35], [36].
 |
The Conceptual Graph shown in Figure 5.18 shows how to capture a resolved ambiguity about the existence of “a sailor”, which might be in the real world, or possibly just one agent’s belief context. The graph and its CGIF equivalent express that it is in both Tom and Mary’s belief context, but not necessarily the real world. Conceptual graphs have also been used to represent sentences in legal statutes, which can have complex quantification in the form of exceptions or exclusions, e.g., “The Plaintiff by a warranty deed conveyed the land to the Defendant, save and except for all oil, gas and other minerals.”, which might be handled by creating a negated type restriction or a negated context.
 |
 |
Graph-based semantic representation for Natural Language have a long history, including work by many pioneers of Computer Science and Artificial Intelligence including John Sowa[37], Roger Schank, Ronald Brachman, and Stuart Shapiro[38], who themselves drew inspiration from the work of Charles S. Pierce in the 1880’s on “Existential Graphs” and graph-based inference. The advantages that graphs offer over logics are that the mapping of natural language sentences to graphs can be more direct and structure sharing can be used to make it clear when the interpretation of two expressions correspond to the same entity, which allows quantifiers to span multiple clauses. Graphs can also be more expressive, while preserving the sound inference of logic. One can distinguish the name of a concept or instance from the words that were used in an utterance. Also, many known restrictions of first order logic, such as its limited set of quantifiers and connectives, the reliance on implication and inference to express class membership, the limited scope of quantifiers, and difficulties in representing questions and requests can all be addressed in a graphical representation. Other scope issues, such as subjective context can also be disambiguated.
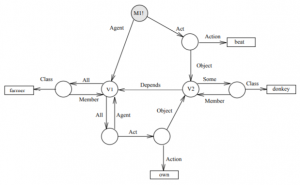
The SNePS framework has been used to address representations of a variety of complex quantifiers, connectives, and actions, which are described in The SNePS Case Frame Dictionary and related papers. For example, Figure 5.19 shows how a graph might represent the sentence “All men are mortal” without implication (or its equivalent as disjunction), how a graph might represent the correct quantifier scope in the expression “Every farmer that owns a donkey beats it.”, and a graph for expressing a quantifier that means that “at least I and at most j of a given set of statements are true”. SNePS also included a mechanism for embedding procedural semantics, such as using an iteration mechanism to express a concept like, “While the knob is turned, open the door”.

|
|

|
The most recent projects based on SNePS include an implementation using the Lisp-like programming language, Clojure, known as CSNePS or Inference Graphs[39], [40]. It is being used to represent clinical practice guidelines[41]. Clinical guidelines are statements like “Fluoxetine (20–80 mg/day) should be considered for the treatment of patients with fibromyalgia.” [42], which are disseminated in medical journals and the websites of professional organizations and national health agencies, such as the U.S. Preventive Services Task Force and the U.S. Agency for Health Research Quality (AHRQ), respectively as sentences, but must be mapped onto some actionable format if they are to be used to generate notifications within a clinical decision support system or to automatically embed so-called “infobuttons” within electronic medical records[43], [44].
5.4 Summary
- Minsky, M. (1975). A Framework for Representing Knowledge. In P. Winston, Ed., The Psychology of Computer Vision. New York: McGraw-Hill, pp. 211-277. A copy of the original paper, published as an MIT Memo, can be found online as https://courses.media.mit.edu/2004spring/mas966/Minsky%201974%20Framework%20for%20knowledge.pdf ↵
- Brewka, G. (1987). The Logic of Inheritance in Frame Systems. In Proceedings of the International Joint Conference on Artificial Intelligence. ↵
- AI frame systems are similar to object oriented programs (OOP), as AI frames provided much of the basis for early OOP. ↵
- Bar-Haim, R., Dagan, I., Greental, I., & Shnarch, E. (2007). Semantic Inference at the Lexical-Syntactic Level. In Proceedings of the National Conference on Artificial Intelligence (Vol. 22, No. 1, p. 871). Menlo Park, CA; Cambridge, MA; London; AAAI Press; MIT Press. ↵
- Dowty, D. R., Wall, R., & Peters, S. (2012). Introduction to Montague semantics (Vol. 11). Springer Science & Business Media. ↵
- Barwise, J., & Cooper, R. (1981). Generalized Quantifiers and Natural Language. In Philosophy, language, and artificial intelligence (pp. 241-301). Springer, Dordrecht. ↵
- Noy, N. F., Musen, M. A., Mejino Jr., J.L.V, and Rosse, C. (2004). Pushing the Envelope: Challenges in a Frame-Based Representation of Human Anatomy. Data & Knowledge Engineering Volume 48, Issue 3, March 2004, Pages 335-359 ↵
- Baader, F., Calvanese, D., McGuinness, D., Patel-Schneider, P., and Nardi, D. (Eds.). (2003). The Description Logic Handbook: Theory, Implementation and Applications. Cambridge University Press. ↵
- Musen, M. A., and the Protégé Team (2015). The Protégé Project: A Look Back and a Look Forward. AI Matters, 1(4), 4–12. https://doi.org/10.1145/2757001.2757003. PMID: 27239556 ↵
- Barwise, J. and Cooper, R. (1981). Generalized Quantifiers and Natural Language. Linguistics and Philosophy Vol. 4 ↵
- Johnson-Laird, P. N. (1977). Procedural Semantics. Cognition, 5(3), 189-214. ↵
- Woods, W. A. (1981). Procedural Semantics as a Theory of Meaning. Bolt, Beranek and Newman, Inc. Cambridge, MA. ↵
- Miller, G. A. (1974). Toward a Third Metaphor for Psycholinguistics. In W. B. Weimer & D. S. Palermo (Eds.), Cognition and the Symbolic Processes. Lawrence Erlbaum. ↵
- Johnson-Laird, P. N. (1977). Procedural Semantics. Cognition, 5(3), 189-214. ↵
- Besta, M., Peter, E., Gerstenberger, R., Fischer, M., Podstawski, M., Barthels, C., ... & Hoefler, T. (2020). Demystifying Graph Databases: Analysis and Taxonomy of Data Organization, System Designs, and Graph Queries. arXiv preprint arXiv:1910.09017v4 URL https://arxiv.org/abs/1910.09017v4 (Accessed March 2021). ↵
- Hogan, A., Blomqvist, E., Cochez, M., d'Amato, C., de Melo, G., Gutierrez, C., ... & Zimmermann, A. (2020). Knowledge Graphs. arXiv preprint arXiv:2003.02320. ↵
- Sun, C. (2018) A Natural Language Interface for Querying Graph Databases Masters Thesis, Computer Science and Engineering, Massachusetts Institute of Technology. ↵
- Church, A. (1941). The Calculi of Lambda-Conversion. Princeton University Press. ↵
- Montague, R. (1974). Formal Philosophy: Selected Papers of Richard Montague. Yale University Press ↵
- Dowty, D., Wall, R. and Peters, S. (1981) Introduction to Montague Semantics. Dordrecht: D. Reidel. ↵
- Chierchia G. and McConnell-Ginet, S. (1990). Meaning and Grammar - 2nd Edition: An Introduction to Semantics. The MIT Press. ↵
- . By new symbols, I mean things like cat1, cat2, etc. which are returned by the Common Lisp function gensym(). ↵
- Baader, F., Calvanese, D., McGuinness, D., Patel-Schneider, P., Nardi, D. (eds.) (2003) The Description Logic Handbook: Theory, Implementation and Applications. Cambridge University Press. ↵
- Lassila, O. and Swick, R.R. (1998). Resource description framework (RDF) model and syntax specification. ↵
- McBride, B. (2004). The Resource Description Framework (RDF) and Its Vocabulary Description Language RDFS. In Handbook on Ontologies (pp. 51-65). Springer, Berlin, Heidelberg. ↵
- Bechhofer, S., Van Harmelen, F., Hendler, J., Horrocks, I., McGuinness, D.L., Patel-Schneider, P.F. and Stein, L.A. (2004). OWL Web Ontology Language Reference. W3C recommendation, 10(02). ↵
- Antoniou, G. and Van Harmelen, F. (2004). Web Ontology Language: OWL. In Handbook on Ontologies (pp. 67-92). Springer, Berlin, Heidelberg. ↵
- Roy, J. and Ramanujan, A. (2001). XML Schema Language: Taking XML to the Next Level. IT Professional, 3(2), pp.37-40. ↵
- Cycorp is the company that maintains and distributes Cyc. See https://www.cyc.com/. For a technical overview, see https://www.cyc.com/cyc-technology-overview/ ↵
- Hirst, G. (1992). Semantic Interpretation and the Resolution of Ambiguity. Cambridge University Press. ↵
- Charniak, E. (1981). A common representation for problem-solving and language-comprehension information. Artificial Intelligence, 16(3), 225-255. ↵
- Lopatovska, I., Rink, K., Knight, I., Raines, K., Cosenza, K., Williams, H., Sorsche, P., Hirsch, D., Li, Q., and Martinez, A. (2019). Talk to Me: Exploring User Interactions with the Amazon Alexa. Journal of Librarianship and Information Science, 51(4), 984-997. ↵
- Kollar, T., Berry, D., Stuart, L., Owczarzak, K., Chung, T., Kayser, M., Snow, B., and Matsoukas, S. (2018). The Alexa Meaning Representation Language. In Proceedings of the 16th Annual Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT 2018), pages 177–184 ↵
- Perera, V., Chung, T., Kollar, T., & Strubell, E. (2018). Multi-Task Learning For Parsing The Alexa Meaning Representation Language. Proceedings of the AAAI Conference on Artificial Intelligence, 32(1). ↵
- Gkiokas, A., & Cristea, A. I. (2014). Training a Cognitive Agent to Acquire and Represent Knowledge from RSS Feeds onto Conceptual Graphs. IARIA COGNITIVE, pp. 184-194. ↵
- From their 2014 work, Gkiokas and Cristea provide 7MB of manually transcribed CG structures for data obtained from RSS feeds from BBC, SkyNews, KnoxNews, USA Today and Science Daily that they make available online at: https://github.com/alexge233/conceptual_graph_set ↵
- John Sowa is most associated with Conceptual Graphs, which he summarizes on his webpage: http://www.jfsowa.com/cg/cgif.htm ↵
- Stuart Shapiro is most associated with SNePs. An excellent summary of Semantic Networks, including SNePS was written by J. Martins. It is available online at: https://web.archive.org/web/20190413011355/https://fenix.tecnico.ulisboa.pt/downloadFile/3779571243569/Cap6.pdf ↵
- Schlegel, D. R., and Shapiro, S. C. (2013). Inference Graphs: A Roadmap. In Poster collection of the Second Annual Conference on Advances in Cognitive Systems (pp. 217-234). ↵
- Schlegel, D., and Shapiro, S. (2015). Inference Graphs: Combining Natural Deduction and Subsumption Inference in a Concurrent Reasoner. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 29, No. 1). ↵
- Schlegel, D. R., Gordon, K., Gaudioso, C., and Peleg, M. (2019). Clinical Tractor: A Framework for Automatic Natural Language Understanding of Clinical Practice Guidelines. In AMIA Annual Symposium Proceedings (Vol. 2019, p. 784). American Medical Informatics Association. ↵
- Gad El-Rab, W., Zaïane, O. R., & El-Hajj, M. (2017). Formalizing Clinical Practice Guideline for Clinical Decision Support Systems. Health Informatics Journal, 23(2), 146-156. ↵
- Cook, D. A., Teixeira, M. T., Heale, B. S., Cimino, J. J., & Del Fiol, G. (2017). Context-Sensitive Decision Support (Infobuttons) in Electronic Health Records: A Systematic Review. Journal of the American Medical Informatics Association : JAMIA, 24(2), 460–468. https://doi.org/10.1093/jamia/ocw104 ↵
- Hematialam, H., & Zadrozny, W. (2017). Identifying Condition-Action Statements in Medical Guidelines Using Domain-Independent Features. ArXiv, abs/1706.04206. ↵
The Unified Verb Index is a federated system which merges links and web pages from four different natural language processing projects related to verbs: VerbNet, PropBank, FrameNet, and OntoNotes Sense Groupings.