Chapter 24 Section 24.3: Tests of General Relativity
24.3 Tests of General Relativity
Learning Objectives
By the end of this section, you will be able to:
- Describe unusual motion of Mercury around the Sun and explain how general relativity explains the observed behavior
- Provide examples of evidence for light rays being bent by massive objects, as predicted by general relativity’s theory about the warping of spacetime
What Einstein proposed was nothing less than a major revolution in our understanding of space and time. It was a new theory of gravity, in which mass determines the curvature of spacetime and that curvature, in turn, controls how objects move. Like all new ideas in science, no matter who advances them, Einstein’s theory had to be tested by comparing its predictions against the experimental evidence. This was quite a challenge because the effects of the new theory were apparent only when the mass was quite large. (For smaller masses, it required measuring techniques that would not become available until decades later.)
When the distorting mass is small, the predictions of general relativity must agree with those resulting from Newton’s law of universal gravitation, which, after all, has served us admirably in our technology and in guiding space probes to the other planets. In familiar territory, therefore, the differences between the predictions of the two models are subtle and difficult to detect. Nevertheless, Einstein was able to demonstrate one proof of his theory that could be found in existing data and to suggest another one that would be tested just a few years later.
The Motion of Mercury
Of the planets in our solar system, Mercury orbits closest to the Sun and is thus most affected by the distortion of spacetime produced by the Sun’s mass. Einstein wondered if the distortion might produce a noticeable difference in the motion of Mercury that was not predicted by Newton’s law. It turned out that the difference was subtle, but it was definitely there. Most importantly, it had already been measured.
Mercury has a highly elliptical orbit, so that it is only about two-thirds as far from the Sun at perihelion as it is at aphelion. (These terms were defined in the chapter on Orbits and Gravity.) The gravitational effects (perturbations) of the other planets on Mercury produce a calculable advance of Mercury’s perihelion. What this means is that each successive perihelion occurs in a slightly different direction as seen from the Sun (Figure 1).
Mercury’s Wobble.
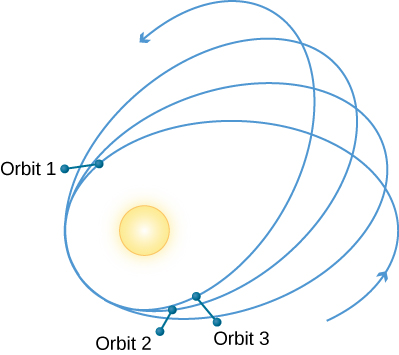
Figure 1. The major axis of the orbit of a planet, such as Mercury, rotates in space slightly because of various perturbations. In Mercury’s case, the amount of rotation (or orbital precession) is a bit larger than can be accounted for by the gravitational forces exerted by other planets; this difference is precisely explained by the general theory of relativity. Mercury, being the planet closest to the Sun, has its orbit most affected by the warping of spacetime near the Sun. The change from orbit to orbit has been significantly exaggerated on this diagram.
According to Newtonian gravitation, the gravitational forces exerted by the planets will cause Mercury’s perihelion to advance by about 531 seconds of arc (arcsec) per century. In the nineteenth century, however, it was observed that the actual advance is 574 arcsec per century. The discrepancy was first pointed out in 1859 by Urbain Le Verrier, the codiscoverer of Neptune. Just as discrepancies in the motion of Uranus allowed astronomers to discover the presence of Neptune, so it was thought that the discrepancy in the motion of Mercury could mean the presence of an undiscovered inner planet. Astronomers searched for this planet near the Sun, even giving it a name: Vulcan, after the Roman god of fire. (The name would later be used for the home planet of a famous character on a popular television show about future space travel.)
But no planet has ever been found nearer to the Sun than Mercury, and the discrepancy was still bothering astronomers when Einstein was doing his calculations. General relativity, however, predicts that due to the curvature of spacetime around the Sun, the perihelion of Mercury should advance slightly more than is predicted by Newtonian gravity. The result is to make the major axis of Mercury’s orbit rotate slowly in space because of the Sun’s gravity alone. The prediction of general relativity is that the direction of perihelion should change by an additional 43 arcsec per century. This is remarkably close to the observed discrepancy, and it gave Einstein a lot of confidence as he advanced his theory. The relativistic advance of perihelion was later also observed in the orbits of several asteroids that come close to the Sun.
Deflection of Starlight
Einstein’s second test was something that had not been observed before and would thus provide an excellent confirmation of his theory. Since spacetime is more curved in regions where the gravitational field is strong, we would expect light passing very near the Sun to appear to follow a curved path (Figure 2), just like that of the ant in our analogy. Einstein calculated from general relativity theory that starlight just grazing the Sun’s surface should be deflected by an angle of 1.75 arcsec. Could such a deflection be observed?
Curvature of Light Paths near the Sun.
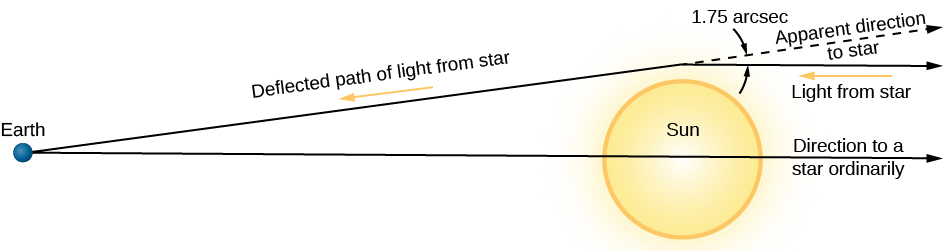
Figure 2. Starlight passing near the Sun is deflected slightly by the “warping” of spacetime. (This deflection of starlight is one small example of a phenomenon called gravitational lensing, which we’ll discuss in more detail in The Evolution and Distribution of Galaxies.) Before passing by the Sun, the light from the star was traveling parallel to the bottom edge of the figure. When it passed near the Sun, the path was altered slightly. When we see the light, we assume the light beam has been traveling in a straight path throughout its journey, and so we measure the position of the star to be slightly different from its true position. If we were to observe the star at another time, when the Sun is not in the way, we would measure its true position.
We encounter a small “technical problem” when we try to photograph starlight coming very close to the Sun: the Sun is an outrageously bright source of starlight itself. But during a total solar eclipse, much of the Sun’s light is blocked out, allowing the stars near the Sun to be photographed. In a paper published during World War I, Einstein (writing in a German journal) suggested that photographic observations during an eclipse could reveal the deflection of light passing near the Sun.
The technique involves taking a photograph of the stars six months prior to the eclipse and measuring the position of all the stars accurately. Then the same stars are photographed during the eclipse. This is when the starlight has to travel to us by skirting the Sun and moving through measurably warped spacetime. As seen from Earth, the stars closest to the Sun will seem to be “out of place”—slightly away from their regular positions as measured when the Sun is not nearby.
A single copy of that paper, passed through neutral Holland, reached the British astronomer Arthur S. Eddington, who noted that the next suitable eclipse was on May 29, 1919. The British organized two expeditions to observe it: one on the island of Príncipe, off the coast of West Africa, and the other in Sobral, in northern Brazil. Despite some problems with the weather, both expeditions obtained successful photographs. The stars seen near the Sun were indeed displaced, and to the accuracy of the measurements, which was about 20%, the shifts were consistent with the predictions of general relativity. More modern experiments with radio waves traveling close to the Sun have confirmed that the actual displacements are within 1% of what general relativity predicts.
The confirmation of the theory by the eclipse expeditions in 1919 was a triumph that made Einstein a world celebrity.
Key Concepts and Summary
In weak gravitational fields, the predictions of general relativity agree with the predictions of Newton’s law of gravity. However, in the stronger gravity of the Sun, general relativity makes predictions that differ from Newtonian physics and can be tested. For example, general relativity predicts that light or radio waves will be deflected when they pass near the Sun, and that the position where Mercury is at perihelion would change by 43 arcsec per century even if there were no other planets in the solar system to perturb its orbit. These predictions have been verified by observation.

